Pourquoi sommes-nous plus susceptibles d’attraper un coup de soleil lorsque nous portons des lunettes de soleil ? Pourquoi le chocolat nous rend-il plus intelligents ?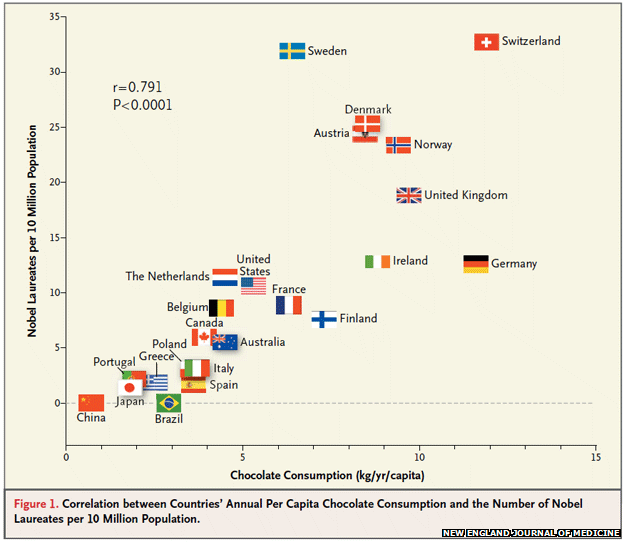

Ce sont les questions que l’on peut se poser après avoir appris que l’augmentation du nombre de coups de soleil suivait l’évolution des ventes de lunettes de soleil, ou suite à l’observation du graphique ci-contre…              Mais il faudrait d’abord se demander s’il y a réellement un lien de cause à effet entre les deux données comparées !

Les statistiques sont en effet un outil à manipuler avec précaution, car il est facile d’interpréter les chiffres de manière erronée.

Alors, quelles sont les bonnes questions à se poser face à un journal qui proclame, par exemple, « Pour avoir un prix Nobel, mangez du chocolat » ?

• D’où vient l’information ?

Tout journal aspire à être lu. Et pour cela, un titre accrocheur fonctionne bien mieux que de longues explications prudentes ! Ainsi, si l’article du Dr. Messerli (qui a mené l’étude sur le potentiel effet du chocolat sur l’intelligence) explique que « reste à déterminer si la consommation de chocolat est, ou non, le mécanisme sous-jacent de l’association observée avec une fonction cognitive améliorée », la plupart des journaux se passent de telles nuances… D’où l’intérêt de rechercher la source première de l’information – ce qui permet de plus d'en vérifier la fiabilité.

• Y a-t-il un sens à mettre en relation les deux valeurs comparées ?

Du graphique ci-dessus, on pourrait déduire que la diminution de la consommation de margarine fait baisser le taux de divorce dans le Maine… Mais cela paraît étrange, n’est-ce pas ? En effet, certaines valeurs ne sont corrélées que par hasard. Pour pouvoir relier deux valeurs, il faut d’abord que l’on puisse supposer un lien entre les deux : aujourd’hui, on peut comparer rapidement un très grand nombre de données, pour aboutir à des corrélations farfelues, comme entre la consommation de fromage et le nombre de morts par entortillement dans des draps de lit ! 

(Pour faire le plein de corrélations aussi absurdes qu’amusantes, en anglais : Spurious correlations )

• Peut-on relier les deux variables à un facteur commun ?

Parfois, la corrélation entre deux valeurs n’est pas le fruit d’une relation directe entre elles : leur évolution est due à un autre facteur, qui les fait augmenter ou diminuer de concert. Pour reprendre l’exemple du début, porter des lunettes de soleil ne nous rend pas plus sensibles aux insolations, et ce n’est pas le fait d’attraper un coup de soleil qui nous fait porter des verres sombres… L’évolution des deux valeurs est plus probablement due à l’augmentation de l’ensoleillement estival ! De même, on peut relier l’acquisition de prix Nobel et la consommation de chocolat – produit « de luxe » – au niveau de développement d’un pays.

• Y a-t-il des biais statistiques ?

Si l’interprétation des données joue un grand rôle dans la justesse des résultats, les données elles-mêmes peuvent être plus ou moins représentatives du sujet d’étude : dans l’exemple de l’effet du chocolat sur l’intelligence, le graphique tracé est celui du nombre de prix Nobel par million d’habitants, en fonction de la consommation annuelle moyenne de chocolat par personne. Cependant, ainsi que le mentionne Franz Messerli, rien n’indique la consommation de chaque lauréat du prix Nobel, ce qui remet en partie en cause l’action du chocolat sur leur intelligence.

De manière plus générale, les données proviennent toujours d’un échantillon de la population, et de la taille de ce dernier dépend la fiabilité de l’étude – plus l’échantillon est petit, moins il est représentatif de la population globale…

Bref, vous l’aurez compris, les statistiques sont un outil que l’on peut facilement faire mentir. Il est donc important de ne pas aller trop vite dans l’interprétation des données et de toujours garder un regard critique sur ce que l’on peut lire ! Si vous souhaitez en savoir plus sur les biais statistiques, voici une vidéo intéressante sur le paradoxe de Simpson – pourquoi un même phénomène observé sur différents groupes semble parfois s’inverser lorsqu’on réunit les groupes : Le paradoxe de Simpson - Science étonnante (vidéo)

Sources :

Pas de lauréat, pas de chocolat : Méfiez-vous des statistiques

Drôles de statistiques

Chocolate Consumption, Cognitive Function, and Nobel Laureates

Spurious correlations